[논문리뷰] DDPM : Denoising Diffusion Probabilistic Models

https://arxiv.org/pdf/2006.11239.pdf

https://github.com/hojonathanho/diffusion

GitHub - hojonathanho/diffusion: Denoising Diffusion Probabilistic Models

 

 

Contents

1. Subject

2. Intro

3. Background

   3-1. Forward(diffusion) process : q

   3-2. Reverse(denoising) process : p

   3-3. Loss Function

4. Method

5. Results

6. Discussion

 

---

 

1. Subject

 

 

Denoising Diffusion Probabilistic Models

영상의 디노이징에 사용되는 확산 확률 모델

 

열역학에서 영감을 받은 확산 확률 모델을 사용하여 고품질의 이미지 합성 방법을 제시한다.

 

 

---

2. Intro

디퓨저

시간이 지날수록 방 전체에 향기가 확산된다.

t라는 짧은 시간동안 움직인 분자의 위치는 확률 분포를 따른다.

 

 

Markov Chain

t+1의 확률은 t에 의존한다.

= 바로 전 단계의 상태에서만 영향을 받는다.

 

 

---

3. Background

 

 

 

3-1. Forward process (q)

= diffusion process

 

주어진 이미지가 x_0이고, 그로부터 noise를 추가하는 과정이 q이다.

x_0에 noise를 추가하면 x_1이 되고, 그 과정을 q(x_1|x_0)로 표현한다. 

이를 시간 t에 대한 general 한 식으로 표현하면 q(x_t|x_t-1)이다.

​

 

 

q(x1:T|x0) : 초기조건 x0이 주어졌을 때, 시간 t=1에서 T까지의 조건부 확률 분포

q(xt | xt−1) := N(xt; (1 − βt)xt−1, βtI)

: x_t-1이 주어졌을 때, t_x로의 전이 확률 분포.

정규분포로 모델링 되면

평균 μ는 (1 − βt)xt−1이고, 공분산 행렬은 βtI. (I는 단위 행렬)

 

β가 1에 가까울수록 x_t-1의 항이 0에 가까워지므로 이전 정보가 적고 노이즈가 증가함.

= β가 0에 가까울수록 노이즈가 적음.

 

---

3-2. Reverse process (p)

= denoising process

 

 

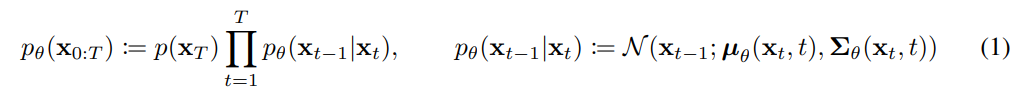
p(x_(t-1) | x_t)   : noise에서 image로의 방향, t에서 t-1의 시간만큼

 

forward process가 가우시안이면, backward process도 가우시안이 된다(증명완료)

 

 

 

 

mean, variance를 예측해야함.p는 학습시켜야 하는 inverse모델

 

 

---

3-3. Loss Function

x_t 가 주어졌을 때

x_(t-1) 을 예측할 수 있다면

x_0   또한 예측할 수 있다.

 

 

Loss function을 풀면 위와 같은 식이 나온다.

 

L_t : regularization term으로 베타t를 학습시킴

L_t-1: reconstruction term으로 매 단계에서 noise를 지움

L_0 : reconstruction term으로 최종 이미지를 생성

 

여기서 가장 중요한 term은 L_t-1

X_0부터 시작해서 식을 전개하면 q식의 정규분포를 알 수 있다.

이를 바탕으로 Dkl 

 

 

 

---

4. Method

 

DDPM에서는 베타를 상수로 고정한다. 따라서 L_T를 고려하지 않아도 된다.

베타의 역할은 이미지에 추가되는 노이즈의 강도를 조절하는 것인데, 이를 고정함으로 모델의 안정성과 효율을 높인다.

 

 

 

 

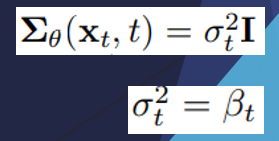
P의 variance도 상수 행렬로 정의하여 학습이 필요하지 않게 했다.

 

 

 

 

µθ를 구하면 이를 활용해서 xt−1을 샘플링 할 수 있다.

 

 

 

 

정리해보면,

   1) β를 상수로 fix

   2) p의 variance fix

   3) μ를 residual 식으로 변경

을 적용하면 아래처럼

 

이 식이,

이렇게 심플하게 정리된다.

simplify loss function은 ϵ의 식으로 정리되어

MSE, denoising식이 된다.

 

 

 

 

 

Training

Noise를 더해나가면서 Noise(ϵ)가 얼마나 추가되었는지를 학습한다.

학습 시 특정 step에서 gaussian noise가
얼마나 추가되었는지 예측하도록 학습한다.

 

 

 

Sampling

학습이후 gaussian noise 에서부터 순차적으로 denoising한다.

 

 

---

6. Results

 

• Is : inception score 얼마나 특정 class로의 추정을 잘 하는지
• FID : 실제 데이터와의 유사도

 

 

reverse process를 통해 Image로 복원하는 과정

 

두 이미지 Interpolation

 

 

 

 

---

6. Discussion

- 열역학에 기반한 이론을 응용하여 vision 기술에 접목한 점

- 기존에 증명된 문제들로 식의 단순화를 통해 성능을 높임

 

 

 

 

 

 

Reference

(Youtube) PR-409: Denoising Diffusion Probabilistic Models (Hyeongmin Lee)

DDPM: Denoising Diffusion Probabilistic Model  (Jang. Inspiration)

https://jang-inspiration.com/ddpm-2